UN'ESERCITAZIONE
DI FISICA CON IL F�HN
Articolo
tratto da NIMBUS 13/14,
Giugno 1998
In questo articolo � riportata una parte della tesina presentata da
Matteo Richiardone, allievo dell'I.T.C.S. "Blaise Pascal" di Giaveno, nel
corso della maturit� dell'anno scolastico 1996-97. Essa si proponeva lo
studio termodinamico del f�hn, vento di caduta particolarmente presente
nella zona della Val di Susa. Evidentemente questa trattazione non ha la
pretesa di sostituirsi ad un trattato di meteorologia teorica, ma vuole
proporre un'applicazione pratica della fisica che, pur senza tener conto
delle molte variabili che caratterizzano il fenomeno, costituisce un modo
per rendere lo studio di questa disciplina pi� vicino alla realt�
osservabile. Sono stati riportati fra parentesi quadre alcuni commenti non
appartenenti al testo originale.
IL F�HN
Il f�hn � un vento secco e tiepido, spesso impetuoso e a raffiche
irregolari, che scende da una catena montuosa. Non � l'unico esempio di
vento orografico di questo tipo: altrettanto famoso � il chinook, che
spira sul versante orientale delle Montagne Rocciose. Quando esso appare
la temperatura subisce un rapido e sensibile aumento, mentre l'aria
diviene limpida; le nubi sono assenti, a parte quelle di tipo lenticolare,
quasi sempre isolate e con i bordi frastagliati (altocumuli). Il f�hn
soffia prevalentemente d'inverno e in primavera, soprattutto lungo le
vallate alpine dell'Italia settentrionale e anche in piena Valpadana, da
nord verso sud o da nord-ovest verso sud-est. La frequenza di questo
evento � variabile: l'alta Lombardia e il Piemonte, le regioni pi�
interessate dal fenomeno, lo registrano in media una decina di giornate
all'anno [anche 40 giorni se si considerano i micro f�hn della durata di
poche ore].Alla confluenza delle vallate alpine con la pianura padana (ad
esempio all'imbocco della Val di Susa) il f�hn pu� superare la velocit� di
100 km/h. Sull'Italia settentrionale questo vento si manifesta quando la
differenza di pressione atmosferica, o gradiente barico, tra il nord e il
sud delle Alpi � elevata. Solitamente sottovento alla catena alpina �
presente una depressione in movimento verso l'Adriatico, mentre sulla
Svizzera vi � un promontorio di alta pressione in movimento verso sud.
Il f�hn � presente anche sul versante settentrionale delle Alpi; in
questo caso soffia da sud. La distribuzione della pressione atmosferica �
l'esatto contrario di quella sopra descritta, e cio� alti valori in
Valpadana e valori bassi nella zona settentrionale della catena
alpina.
Il manifestarsi di questo fenomeno produce, durante la stagione
invernale e primaverile, il distacco di valanghe, a causa del subitaneo
aumento della temperatura. Presupposto per la genesi del f�hn e di altri
venti analoghi cosiddetti discendenti � la presenza di catene
montuose piuttosto elevate; venti di questo tipo si possono quindi
avere anche lungo i due versantidell'Appennino.
Vediamo in concreto che cosa accade. L'aria che si avvicina alle
montagne � costretta a salire fin sulle creste, da dove poi essa scende a
valle; durante la salita essa diminuisce di temperatura (raffreddamento
adiabatico), mediamente di un grado Celsius ogni 100 m. Nell'aria in
ascesa � presente vapore acqueo che, con il raffreddamento, condensa; si
formano in questo modo nuvole e precipitazioni. Attraverso questo fenomeno
si libera il calore latente di condensazione, che riscalda l'aria; il
raffreddamento adiabatico viene quindi ridotto a circa 0.5 / 0.61�C ogni
100 m di salita. Durante la discesa [sull'altro versante] avviene un
riscaldamento progressivo, in media di 1�C ogni 100 m di perdita di quota,
dovuto al processo di compressione adiabatica. E' facile rendersi conto di
questa situazione se si pensa a ci� che avviene quando si gonfia la ruota
di una bicicletta: anche in questo caso l'aria si riscalda, ma non a causa
degli attriti, come si sarebbe portati a pensare, bens� per la rapidit�
del fenomeno, che impedisce quasi del tutto gli scambi di calore con
l'esterno (vedi trattazione fisica seguente). Immaginando una quota
iniziale pari a quella del livello del mare ed una finale di 3000 metri,
l'andamento della temperatura � quello riportato nella tabella
seguente.
| Raffreddamento adiabatico di 1�C ogni 100 m
sino a quota 1500 m |
=15�C |
| Dai 1500 m in su formazione di nuvole con
raffreddamento di 0.5�C ogni 100 m |
=7.5�C |
| Riscaldamento adiabatico a valle di 1�C ogni
100 m |
=30�C |
| Eccedenza termica |
=7.5�C |
Qui le caratteristiche della massa d'aria non svolgono alcun ruolo. Il
f�hn, dunque, non � di per s� un vento caldo, ma l'aumento di temperatura
subita dall'aria durante la discesa verso valle deriva dal riscaldamento
prodotto durante il processo descritto. Le osservazioni compiute sulle
Alpi indicano che in caso di f�hn si hanno venti e precipitazioni lungo il
versante sopravvento ove avviene l'ascesa forzata dell'aria (fenomeno di
stau - cos� lo definiscono i meteorologici tedeschi -che significa
sbarramento) mentre in Valpadana il tempo � sereno e molto secco. La
diminuzione dell'umidit� relativa � un evento anch'esso collegato
all'aumento della temperatura. Il f�hn pu� durare due o tre giorni [o
poche ore], e sulla pianura padana � seguito da un forte abbassamento
della temperatura notturna. In primavera il f�hn � spesso seguito da
gelate dannose per le colture; ci� avviene perch� la massa d'aria
originaria � di estrazione polare osubpolare e, quando cessano le
condizioni di riscaldamento per compressione, si evidenzia la vera natura
dell'aria sopraggiunta. Il f�hn della pianura padana � indice di una
situazione meteorologica molto dinamica e foriera di perturbazioni per
l'Italia centromeridionale. Infatti, appena termina l'azione di questo
vento, gi� nella parte di pianura a ridosso dell'Appennino settentrionale
il cielo si rannuvola perch� si evidenzia la natura turbolenta e instabile
della massa d'aria giunta d'oltralpe. Ad aggravare l'evoluzione del tempo
contribuisce la presenza di depressioni sull'Adriatico o sul Tirreno con
conseguente richiamo da sud di aria pi� calda che viene a contrastare
quella fredda. Solitamente il maltempo, quando dalle Alpi soffia il f�hn,
� pi� accentuato lungo il versante adriatico dell'Appennino.
LEGGI FISICHE VALIDE PER IL FENOMENO DEL
F�HN
Come detto in precedenza il modello teorico che descrive pi� fedelmente
il processo fisico del f�hn � quello di una trasformazione adiabatica,
ovvero senza scambi di calore con l'esterno. Per questo motivo la prima
legge della termodinamica:
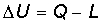
essendo Q = 0 si riduce a:
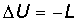
ove L indica il lavoro fatto dal sistema (>0) o fatto sul
sistema (<0) e 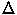 rappresenta la
variazione di energia interna di un gas perfetto. Nel nostro caso il
lavoro � fatto sul sistema (compressione) e perci�
rappresenta la
variazione di energia interna di un gas perfetto. Nel nostro caso il
lavoro � fatto sul sistema (compressione) e perci� 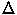 risulter�
positivo. Naturalmente, sempre per quanto riguarda il nostro esperimento,
bisogna supporre che l'aria si comporti come un gas perfetto, e tutto ci�
porter� necessariamente ad errori nella previsione teorica.
risulter�
positivo. Naturalmente, sempre per quanto riguarda il nostro esperimento,
bisogna supporre che l'aria si comporti come un gas perfetto, e tutto ci�
porter� necessariamente ad errori nella previsione teorica.
A causa del primo principio della termodinamica possiamo dedurre che
nel nostro caso ad una compressione (diminuzione di quota) corrisponder�
un aumento di temperatura e viceversa. A questo punto, supponendo sempre
di essere in presenza di una trasformazione adiabatica, possiamo assumere
come valida l'equazione di Poisson:
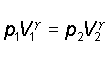
ove il valore di 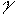 � dato dal
rapporto Cp/Cv dove Cp, rappresenta il calore specifico dell'aria a
pressione costante e Cv il calore specifico a volume costante, mentre p e
V rappresentano rispettivamente la pressione ed il volume della massa
d'aria in questione. La formula scritta precedentemente pu� essere
riportata facendo intervenire le altre due coppie di variabili
termodinamiche:
� dato dal
rapporto Cp/Cv dove Cp, rappresenta il calore specifico dell'aria a
pressione costante e Cv il calore specifico a volume costante, mentre p e
V rappresentano rispettivamente la pressione ed il volume della massa
d'aria in questione. La formula scritta precedentemente pu� essere
riportata facendo intervenire le altre due coppie di variabili
termodinamiche:
1) 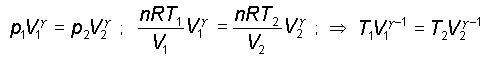
2) 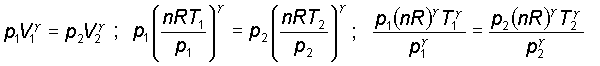
3) 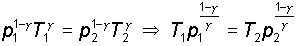
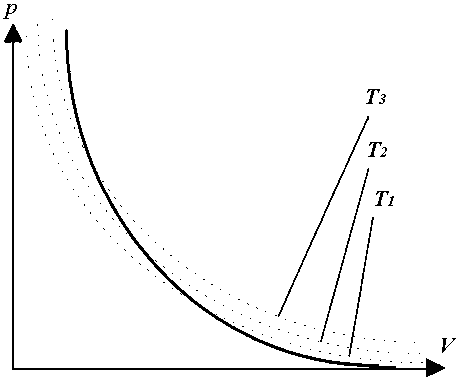
Nella figura seguente � mostrato, su un grafico pressione - volume (p,
V) detto anche diagramma di Clapeyron, l'andamento di tre isoterme (linee
tratteggiate, che rappresentano altrettanti rami di iperbole) con T3 >
T2 > T1, mentre a tratto pieno � rappresentata graficamente
un'adiabatica. Quest'ultima assomiglia ad un'isoterma ma � pi� ripida;
immaginando di comprimere il gas si osserva che la temperatura aumenta, ed
� ci� che avviene praticamente quando si verifica il fenomeno dei
f�hn.
Per procedere con il nostro lavoro sperimentale potremo pertanto
avvalerci dell'equazione precedentemente ricavata, esplicitando il valore
di T2 che � quello che vogliamo ricavare teoricamente:
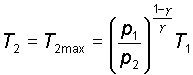
DESCRIZIONE DELLE STAZIONI METEOROLOGICHE
UTILIZZATE
[Per condurre quest'esperienza sono stati utilizzati i dati giornalieri
di temperatura, pressione e umidit� relativa rilevati dalle stazioni
automatiche della rete di rilevamento della Regione Piemonte, lungo la
Valle di Susa, e pubblicati negli Annali Meteorologici regionali
(1992-93). Si sono considerate le seguenti stazioni che si dispongono su
un asse vallivo di circa 90 km di lunghezza:
| Comune |
Denominazione e codice regionale |
Quota m |
| Bardonecchia |
CAMINI FREJUS (11) |
1800 |
| Salbertrand |
GRAN BOSCO � LE SELLE (19) |
1950 |
| Bardonecchia |
PRERICHARD (152) |
1353 |
| Torino |
BUON PASTORE (153) |
240 |
Sebbene la valle sia dotata di numerose altre stazioni, per il nostro
lavoro � stato possibile il solo utilizzo di quattro di esse, in quanto le
altre non sono dotate del barometro che fornisce i dati a noi
indispensabili sulla pressione atmosferica.
[Nella prima casella � riportato il giorno in cui si � verificato il
fenomeno di f�hn; sono stati analizzati i valori riguardanti 6 eventi]
TABELLE DEI DATI SPERIMENTALI E TEORICI RIGUARDANTI LE GIORNATE DI
F�HN
Dati
rilevati
| 01/01/92 |
Quota |
t min |
t max |
t media |
p min |
p max |
u.r. |
pioggia |
| Staz. 11 |
1800 |
n.d. |
n.d. |
n.d. |
n.d. |
n.d. |
n.d. |
No |
| Staz. 152 |
1353 |
-2,8 |
8,7 |
1 |
880 |
884 |
884 |
No |
| Staz. 19 |
1950 |
-0,2 |
7,3 |
3,3 |
810 |
815 |
815 |
No |
| Staz. 153 |
240 |
-2,7 |
7,2 |
1,1 |
1004 |
1004 |
1004 |
No |
Valori
previsti
| |
t max prevista |
Errore assoluto (�C) |
Errore relativo % |
|
t min prevista |
Errore assoluto (�C) |
Errore relativo % |
| Da 11 a 152 |
/ |
/ |
/ |
Da 11 a 152 |
/ |
/ |
/ |
| Da 152 a 19 |
1,3 |
-5 |
-1,78 |
Da 152 a 19 |
-9,1 |
-8,9 |
-3,26 |
| Da 19 a 153 |
14,4 |
17,2 |
6,14 |
Da 19 a 153 |
17 |
19,7 |
7,28 |
| Da 11 a 153 |
/ |
/ |
/ |
Da 11 a 153 |
/ |
/ |
/ |
Dati
rilevati
| 14/03/92 |
Quota |
t min |
t max |
t media |
p min |
p max |
u.r. |
pioggia |
| Staz. 11 |
1800 |
0,8 |
3,5 |
2,3 |
817 |
824 |
68 |
6,6 |
| Staz. 152 |
1353 |
6,1 |
9 |
7,5 |
860 |
866 |
50 |
0,4 |
| Staz. 19 |
1950 |
0,7 |
4,1 |
2,1 |
792 |
798 |
61 |
No |
| Staz. 153 |
240 |
5,3 |
21 |
12,6 |
976 |
976 |
50 |
No |
Valori previsti
| |
t max prevista |
Errore assoluto (�C) |
Errore relativo % |
|
t min prevista |
Errore assoluto (�C) |
Errore relativo % |
| Da 11 a 152 |
7,4 |
-1,6 |
-0,57 |
Da 11 a 152 |
4,8 |
-1,3 |
-0,47 |
| Da 152 a 19 |
2,5 |
-1,6 |
-0,57 |
Da 152 a 19 |
-0,4 |
-1,1 |
-0,4 |
| Da 19 a 153 |
20,4 |
-0,6 |
-0,2 |
Da 19 a 153 |
17,5 |
12,2 |
4,38 |
| Da 11 a 153 |
17,2 |
-3,8 |
-1,29 |
Da 11 a 153 |
15 |
9,7 |
3,48 |
Dati
rilevati
| 25/01/93 |
Quota |
t min |
t max |
t media |
p min |
p max |
u.r. |
pioggia |
| Staz. 11 |
1800 |
-3,9 |
4,6 |
1 |
822 |
827 |
55 |
No |
| Staz. 152 |
1353 |
0,4 |
9,4 |
5,8 |
867 |
872 |
39 |
No |
| Staz. 19 |
1950 |
-5,3 |
3,9 |
0,5 |
795 |
801 |
48 |
No |
| Staz. 153 |
240 |
1,3 |
19,1 |
8 |
979 |
986 |
62 |
No |
Valori previsti
| |
t max prevista |
Errore assoluto (�C) |
Errore relativo % |
|
t min prevista |
Errore assoluto (�C) |
Errore relativo % |
| Da 11 a 152 |
8,8 |
-0,6 |
-0,21 |
Da 11 a 152 |
0,2 |
-0,2 |
-0,07 |
| Da 152 a 19 |
2,7 |
-1,2 |
-0,43 |
Da 152 a 19 |
6,3 |
-1 |
-0,37 |
| Da 19 a 153 |
20,8 |
1,7 |
0,58 |
Da 19 a 153 |
11 |
9,7 |
3,53 |
| Da 11 a 153 |
18,9 |
-0,2 |
-0,07 |
Da 11 a 153 |
9,8 |
8,5 |
3,1 |
Dati
rilevati
| 19/02/93 |
Quota |
t min |
t max |
t media |
p min |
p max |
u.r. |
pioggia |
| Staz. 11 |
1800 |
-5,2 |
6,9 |
1,2 |
821 |
827 |
38 |
No |
| Staz. 152 |
1353 |
-0,6 |
11,1 |
4,2 |
865 |
873 |
33 |
No |
| Staz. 19 |
1950 |
-5,6 |
6,4 |
1,2 |
795 |
802 |
29 |
No |
| Staz. 153 |
240 |
0,2 |
11 |
5,4 |
979 |
993 |
69 |
No |
Valori previsti
| |
t max prevista |
Errore assoluto (�C) |
Errore relativo % |
|
t min prevista |
Errore assoluto (�C) |
Errore relativo % |
| Da 11 a 152 |
11,2 |
0,1 |
0,03 |
Da 11 a 152 |
-1,2 |
-0,6 |
-0,22 |
| Da 152 a 19 |
4,3 |
-2,1 |
-0,75 |
Da 152 a 19 |
-7,1 |
-1,5 |
-0,56 |
| Da 19 a 153 |
23,9 |
12,9 |
4,54 |
Da 19 a 153 |
10,7 |
10,5 |
3,84 |
| Da 11 a 153 |
21,9 |
10,9 |
3,84 |
Da 11 a 153 |
8,6 |
8,4 |
3,07 |
Dati
rilevati
| 11/12/93 |
Quota |
t min |
t max |
t media |
p min |
p max |
u.r. |
pioggia |
| Staz. 11 |
1800 |
-6,9 |
5,4 |
-3,4 |
819 |
821 |
93 |
0,2 |
| Staz. 152 |
1353 |
-2,6 |
7,8 |
1,1 |
865 |
869 |
75 |
1,8 |
| Staz. 19 |
1950 |
-7 |
3,6 |
-3,2 |
793 |
797 |
71 |
0,6 |
| Staz. 153 |
240 |
-2,7 |
13,5 |
7,2 |
981 |
986 |
53 |
No |
Valori previsti
| |
t max prevista |
Errore assoluto (�C) |
Errore relativo % |
|
t min prevista |
Errore assoluto (�C) |
Errore relativo % |
| Da 11 a 152 |
9,9 |
2,1 |
0,75 |
Da 11 a 152 |
-2,7 |
-0,1 |
-0,03 |
| Da 152 a 19 |
1 |
-2,6 |
-0,95 |
Da 152 a 19 |
-9,2 |
-2,2 |
-0,82 |
| Da 19 a 153 |
20,9 |
7,4 |
2,58 |
Da 19 a 153 |
9,6 |
6,9 |
2,5 |
| Da 11 a 153 |
20,3 |
6,8 |
2,37 |
Da 11 a 153 |
7,2 |
4,5 |
1,63 |
Dati
rilevati
| 21/12/93 |
Quota |
t min |
t max |
t media |
p min |
p max |
u.r. |
pioggia |
| Staz. 11 |
1800 |
-6,5 |
7,8 |
1,3 |
816 |
822 |
66 |
0,2 |
| Staz. 152 |
1353 |
-2,1 |
11,5 |
5,7 |
862 |
867 |
52 |
No |
| Staz. 19 |
1950 |
-6,7 |
5,6 |
0,5 |
791 |
797 |
57 |
No |
| Staz. 153 |
240 |
7,3 |
13,7 |
9,4 |
974 |
982 |
63 |
No |
Valori previsti
| |
t max prevista |
Errore assoluto (�C) |
Errore relativo % |
|
t min prevista |
Errore assoluto (�C) |
Errore relativo % |
| Da 11 a 152 |
12,1 |
0,6 |
0,2 |
Da 11 a 152 |
-2,3 |
-0,2 |
-0,07 |
| Da 152 a 19 |
4,8 |
-0,8 |
-0,29 |
Da 152 a 19 |
-8,6 |
-1,9 |
-0,71 |
| Da 19 a 153 |
22,6 |
8,9 |
3,12 |
Da 19 a 153 |
9,5 |
2,2 |
0,78 |
| Da 11 a 153 |
22,4 |
8,7 |
3,03 |
Da 11 a 153 |
7,3 |
0 |
0 |
Note
- Le temperature sono espresse in �C
- Le pressioni sono espresse in hPa
- L'umidit� relativa � espressa in %
- Le precipitazioni sono misurate in mm
- T = t + 273.15 dove: T= temperatura assoluta misurata in K; t =
temperatura misurata in gradi Celsius; si ha evidentemente: 0�C = 273.15
K
OSSERVAZIONI SUL CONFRONTO DEI DATI SPERIMENTALI CON QUELLI TEORICI
Utilizzando i dati rilevati dalle stazioni meteorologiche ed
avvalendoci dell'equazione di Poisson ci � stato possibile elaborare i
valori delle temperature (minime e massime) per le tre postazioni da noi
esaminate. In particolare:
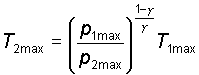
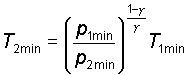
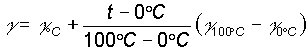
e inoltre:
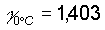 ; ; 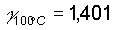
[L'espressione sopra riportata permette di determinare il valore di
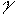 per una data
temperatura t, noti i suoi valori a 0�C e a 100�C, attraverso
l'interpolazione lineare dei valori stessi].
per una data
temperatura t, noti i suoi valori a 0�C e a 100�C, attraverso
l'interpolazione lineare dei valori stessi].
Le previsioni sono state effettuate tra le stazioni contigue nella
tabella, ed in particolare tra la prima posta all'estremit� della Val di
Susa e l'ultima posta a Torino. Per ogni previsione � stato calcolato: 1)
l'errore assoluto, dato dalla differenza tra il valore ottenuto applicando
le leggi fisiche e quello rilevato sperimentalmente; 2) l�errore relativo
percentuale, che � dato dal rapporto tra l'errore assoluto moltiplicato
per 100 ed il valore sperimentale che si voleva determinare. [L'errore
relativo � calcolato sui valori delle temperature in Kelvin, poich�
proprio questi sono i valori che vengono utilizzati nella relazione di
Poisson; vedi equazione riportata sopra]
Dall'analisi dei dati si nota che in alcuni casi il modello teorico ha
prodotto degli eccellenti risultati con errori relativi inferiori
all'unit� percentuale, mentre in altri l'errore � stato decisamente
grossolano. La ragione di queste grandi discrepanze � da ricercarsi nel
fatto che le nostre previsioni sono state effettuate su basi del tutto
teoriche, che perci� non tengono conto delle molte variabili che vanno ad
influenzare il fenomeno naturale [quali ad esempio la presenza di vapore
acqueo che pu� cambiare fase, scambiando con l'ambiente il calore di
evaporazione]. D'altra parte se fosse possibile determinare con esattezza
tutti i valori, quali per esempio quelli di pressione e temperatura, le
previsioni del tempo diventerebbero infallibili e non ci sarebbe pi�
spazio per tutti gli imprevisti cui invece dobbiamo far fronte ogni
giorno. Inoltre bisogna dire che per avere dati sperimentali pi� prossimi
a quelli da noi calcolati si dovrebbe seguire costantemente la stessa
massa d'aria dal momento in cui se ne determina la temperatura iniziale
(nel nostro caso stazione 11) a quello in cui se ne rileva quella finale
(stazione 153), ma purtroppo i dati a disposizione non lo consentono.
Concludendo posso dire che il lavoro svolto � stato piuttosto
interessante e mi ha permesso di scoprire uno dei tanti modi per
utilizzare aspetti teorici della termodinamica, che possono apparire
estremamente astratti, applicandoli ad un esempio pratico.
BIBLIOGRAFIA
LINACRE E. (1992) - Climate Data and Resource, Routledge.
ROTH G.D. (1993) - Meteorologia. Mondadori.
Regione Piemonte - Annale Meteorologico, 1992, 1993.
|